A person’s normal weight is that body weight at which he has the maximum chance of first of all being healthy, and secondly of being attractive in appearance. Compliance with normal indicators does not provide a 100% guarantee of health, but it reduces the risk of diseases and disorders, the risk factor of which is excess body weight. Statistically, those who maintain a normal weight for their height and age feel good even after intense training.
How to calculate normal weight
In reality, optimal weight is an abstract concept that means a certain average value obtained in a calculation that takes into account the physiological parameters of a person:
- height;
- age;
- gender;
- body features.
But when calculating normal weight, individual indicators are not taken into account:
- level of physical activity;
- muscle-fat ratio.
Therefore, the value obtained from the formulas cannot be called as accurate as possible. It is only an approximate guideline that is recommended to be used when monitoring body weight.
The most accurate boundaries of normal weight are considered to be the interval from the minimum to the maximum value, which, according to doctors, a person’s body weight should fall within.
There are several ways to determine normal weight:
- by height;
- by height and age;
- by BMI (body mass index).
Your ideal weight
A woman's weight is considered ideal if:
- does not cause discomfort;
- does not limit a woman when performing everyday activities;
- does not cause health problems;
- does not carry potential risks: the likelihood of developing type 2 diabetes, high blood pressure, high cholesterol, heart disease.
There are various ways to determine your ideal weight. The most common are the following:
- By body mass index. If it is normal and there are no concomitant diseases, there is no need to worry.
- Subtract 110 from your height in centimeters.
- Along the fat fold on the abdomen. The norm for women is 2-4 cm.
- Use an online calculator.
The best way to determine the value of your body mass index is to undergo a comprehensive examination using special equipment. It is available in weight loss clinics. Experts will determine the ratio of fat and muscle mass, ideal weight, indicators necessary to determine the state of health and create a diet.
Calculation by height
The method of calculating normal weight by height is better known as Broca's formula, a French anthropologist. It is the most popular because it is the simplest of all. The formula is considered to be suitable for calculating normal body weight in people with a height of 155 to 185 cm.
How to calculate normal weight taking into account height using the formulas:
- For men: height (cm) - 110.
- For women: height (cm) - 100.
For example, a man’s height is 185 cm. In this case, the norm for him will be considered 185 - 110 = 75 kg. For a woman with a height of 165 cm, a healthy body weight will be 165 - 100 = 65 kg.
We advise you to study: “Why do girls need protein.”
When calculating using these formulas, the following must be taken into account:
- For people 20-30 years old, the calculated value should be reduced by 11%, and for those over 50 years old, it should be increased by 6%.
- Body type. It can be asthenic, normosthenic and hypersthenic. For asthenic, it is necessary to reduce the calculated norm by 10%, and for hypersthenic, on the contrary, increase by 10%.
The criterion for determining body type is the circumference of the wrist of the working hand:
- Asthenic: in women - less than 16 cm, in men - less than 17 cm.
- Normosthenic: in women - 16-18 cm, in men - 17-20 cm.
- Hypersthenic: in women - more than 18 cm, in men - more than 20 cm.
Lorentz formula
There is another way to calculate the normal weight of a woman or man, which takes into account only height. Here the calculation is carried out using the Lorentz formula:
Weight (kg) = (Height (cm) - 100) - (Height (cm) - 150)/2.
For example, for a man 190 cm tall the following are optimal:
(190 - 100) - (190 - 150)/2 = 70 kg.
Share and explore!
Now intuition suggests that it would be correct to separate the two sexes and study separately. After all, in life we often see that men and women have plus or minus different heights and weights
# Men data_male = data[data['Gender'] == 'Male'].copy() # Women data_female = data[data['Gender'] == 'Female'].copy()
Let's take a look at some descriptive statistics that the pandas .
Men:
data_male.describe()
| Height | Weight | |
| count | 5000 | 5000 |
| mean | 175 | 85 |
| std | 7 | 9 |
| min | 148 | 51 |
| 25% | 171 | 79 |
| 50% | 175 | 85 |
| 75% | 180 | 91 |
| max | 201 | 122 |
Women:
data_female.describe()
| Height | Weight | |
| count | 5000 | 5000 |
| mean | 162 | 62 |
| std | 7 | 9 |
| min | 138 | 29 |
| 25% | 157 | 56 |
| 50% | 162 | 62 |
| 75% | 167 | 67 |
| max | 186 | 92 |
A small educational program on the information above
In simple terms:
Descriptive statistics are a set of numbers/characteristics to describe. This is perhaps the easiest type of statistics to understand.
Imagine that you are describing the parameters of a ball. He can be:
- big small
- smooth / rough
- blue red
- bouncy / and not very.
With a strong simplification, we can say that this is what descriptive statistics does . But it does this not with balls, but with data.
Here are the parameters from the table above:
- count — Number of instances.
- mean — Average or sum of all values divided by their number.
- std — Standard deviation or root of variance. Shows the spread of values relative to the average.
- min — Minimum value or minimum.
- 25% — First quartile. Shows the value below which 25% of records are found.
- 50% — Second quartile or median. Shows a value that has the same number of entries above and below it.
- 75% — Third quartile. Similar to the first quartile, but below 75% of records.
- max — Maximum value or maximum.
The average value is very sensitive to outliers! If four people receive a salary of 10,000 rubles, and the fifth - 460,000 rubles. The average will be 100,000 rubles. And the median will remain the same - 10,000 rubles.
This does not mean that average is a bad indicator. You need to treat him more carefully.
By the way, there is also a problem with the median.
If the number of dimensions is odd. Then the median is the value in the middle, if you put the data “by growth”.
And if it’s even, then the median is the average between the two “most central”.
If the data set contains only integers, and the median turns out to be fractional, don’t be surprised. Most likely the number of dimensions is even.
Example:
My son brought home grades from school. There were five lessons, he received: 1, 5, 3, 2, 4 Five grades → odd number Let's sort by height: 1, 2, 3, 4, 5 Take the central one - 3 Median grade - 3
The next day, the son brought new grades from school: 4, 2, 3, 5 Four grades → odd number We build by height: 2, 3, 4, 5 We take the central ones: 3, 4 We find their average: 3.5 Median - 3.5
Conclusion: Well done son 
We see that for men the average and median are: 175 cm and 85 kg. And for women : 162cm and 62kg. This tells us that there are no strong emissions. Or they are symmetrical on both sides of the median. Which happens very rarely.
But both sexes have small deviations of the mean from the median. But they are insignificant and are visible only in hundredths. Go ahead!
Histogram
This is a graph that plots values from minimum to maximum in increasing order, and shows the number of individual instances.
fig, axes = plt.subplots(2,2, figsize=(20,10)) plt.subplots_adjust(wspace=0, hspace=0) axes[0,0].hist(data_male['Height'], label= 'Male Height', bins=100, color='red') axes[0,1].hist(data_male['Weight'], label='Male Weight', bins=100, color='red', alpha= 0.4) axes[1,0].hist(data_female['Height'], label='Female Height', bins=100, color='blue') axes[1,1].hist(data_female['Weight'] , label='Female Weight', bins=100, color='blue', alpha=0.4) axes[0,0].legend(loc=2, fontsize=20) axes[0,1].legend(loc= 2, fontsize=20) axes[1,0].legend(loc=2, fontsize=20) axes[1,1].legend(loc=2, fontsize=20) plt.savefig('plt_histogram.png') plt.show()
The data is distributed in a bell shape. Very similar to a normal distribution.
In addition to statistical tests for normality of distribution, there is a visual test. If the distribution is similar in appearance and logic to normal, we can assume, with some assumptions, that we are dealing with exactly that.
It would be possible to do a statistical test for normality and determine the p-value, but I don’t know how; this is beyond the scope of the article.
Learning to work with hands
Pandas can do a lot of calculations for us. But you need to calculate some statistics yourself at least once. Now I’ll show you how to calculate standard deviation .
Let's do this using the example of men and the characteristic - height.
Average
Formula:
, Where
- M - average value
- N - number of copies
- ni - separate instance
Code:
mean = data_male['Height'].mean() print('mean:\t{:.2f}'.format(mean)) >> mean: 175.33
Average height - 175cm
Squared deviation from the mean
, Where
- di - separate deviation
- ni - separate instance
- M - average
Code:
data_male['Height_d'] = (data_male['Height'] - mean) ** 2 data_male['Height_d'].head(10) >> 0 149.927893 1 0.385495 2 166.739089 3 47.193692 4 4.721246 5 20.288347 6 0.375539 7 2.964214 8 25.997623 9 200.149603 Name: Height_d, dtype: float64
Dispersion
Formula:
, Where
- D - dispersion value
- di - separate deviation
- N - number of copies
Code:
disp = data_male['Height_d'].mean() print('disp:\t{:.2f}'.format(disp)) >> disp: 52.89
Variance - 53
Standard deviation
Formula:
, Where
- std - standard deviation value
- D - dispersion value
Code:
std = disp ** 0.5 print('std:\t{:.2f}'.format(std)) >> std: 7.27
Standard deviation - 7
Confidence intervals
Now we will find out in what height and weight ranges 68%, 95% and 99.7% of men and women fall .
It's not that difficult - you just need to add and subtract the standard deviation from the mean. It looks like this:
- 68% - plus or minus one standard deviation
- 95% - plus or minus two standard deviations
- 99.7% - plus or minus three standard deviations
Let's write a helper function that will count this:
def get_stats(series, title='noname'): # print the title of the characteristic print('= {} =\n'.format(title.upper())) # get descriptive statistics from pandas descr = series.describe() # print the mean mean = descr['mean'] print('= Mean:\t{:.0f}'.format(mean)) # print the standard deviation std = descr['std'] print('= Std:\t {:.0f}'.format(std)) # separator for beauty print('\n= = = =\n') # count intervals ## 68% devi_1 = ## 95% devi_2 = ## 99.7% devi_3 = # print the result print('= 68% is from\t\t{:.0f} to {:.0f}'.format(devi_1[0], devi_1[1])) print('= 95% is from\ t\t{:.0f} to {:.0f}'.format(devi_2[0], devi_2[1])) print('= 99.7% is from\t\t{:.0f} to {:. 0f}'.format(devi_3[0], devi_3[1]))
Well, let’s apply it to the data:
Men | Height
get_stats(data_male['Height'], title='Male Height') >> = MALE HEIGHT = = Mean: 175 = Std: 7 = = = = = 68% is from 168 to 183 = 95% is from 161 to 190 = 99.7% is from 154 to 197
Men | Weight
get_stats(data_male['Height'], title='Male Height') >> = MALE WEIGHT = = Mean: 85 = Std: 9 = = = = = 68% is from 76 to 94 = 95% is from 67 to 103 = 99.7% is from 58 to 112
Women | Height
get_stats(data_male['Height'], title='Male Height') >> = FEMALE HEIGHT = = Mean: 162 = Std: 7 = = = = = 68% is from 155 to 169 = 95% is from 148 to 176 = 99.7% is from 141 to 182
Women | Weight
get_stats(data_male['Height'], title='Male Height') >> = FEMALE WEIGHT = = Mean: 62 = Std: 9 = = = = = 68% is from 53 to 70 = 95% is from 44 to 79 = 99.7% is from 36 to 87
Hence the conclusions:
- Most men: 154cm–197cm and 58kg–112kg.
- Most women: 141cm–182cm and 36kg–87kg.
Now all that remains is to apply machine learning to this set and try to predict weight by height.
Calculation of normal body weight by age and height
As such, there is no formula for normal weight depending on age and height. Here we are talking about a table of ready-made values. It indicates height, age and gender. It is enough to first find your height, then your age and gender, and find the value at the intersection of the required row and column. This will be your optimal body weight. The table below shows the normal weight of a person by age and height.
This formula can be used to calculate weight for most people, except:
- professional athletes;
- pregnant women;
- people suffering from edema and other disorders that lead to excess weight.
Calculation by body mass index
Another popular way to determine a person’s normal weight requires calculating the body mass index (BMI). But this technique is designed a little differently - it does not calculate a specific value of body weight, but determines whether it corresponds to the norm. BMI allows you to assess whether your body weight is overweight, normal or underweight.
The formula for calculating normal weight here is as follows:
BMI = Weight (kg)/Height2 (m).
With a weight of 75 kg and a height of 180 cm, the BMI will be 75/1.8 · 1.8 = 23.15.
The number obtained by the formula remains to be compared with the following values:
- less than 15 - acute lack of weight;
- 15-20 - underweight;
- 20-25 - normal weight;
- 25-30 - overweight;
- 30-35 - 1st degree obesity;
- 35-40 - 2nd degree obesity;
- more than 40 - third degree obesity.
We advise you to study: “Top 5 protein bars for weight loss.”
The optimal weight is considered to be one that corresponds to a BMI of 23. It is the calculation based on body mass index that is the most accurate today. It is designed for ordinary people, taking into account modern living conditions, medical advances and the latest observations. The BMI method is also recommended by WHO.
But the calculated value again turns out to be averaged. For example, athletes and weightlifters may have a higher BMI, but their body weight will not be considered obese. In addition, many who have a normal weight according to their BMI consider themselves overweight. This is possible because the technique does not take into account body type.
With the same BMI, the amount of fat and muscle may be different. Therefore, those who, even with a normal BMI, are not satisfied with their figure, are recommended to simply take up fitness and start following proper nutrition. For those who decide to improve their figure, sports nutrition and dietary products may be useful.
We advise you to study: “The simplest recipes with protein.”
Professional weight and height charts
The Internet is full of various articles and tables on determining the optimal ratio of weight and height. But all of them are very, very conditional, since they do not take into account many factors: age, gender and physiological characteristics of a person. Therefore, excess fat must be assessed not only by the conditional ratios presented in this table, but also by appearance, skin thickness and a number of other factors. With the same height and weight, one person may look plump, while another may look completely normal.
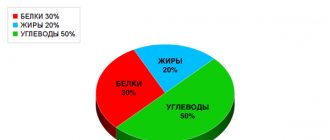
The objective parameter of an ideal body is the percentage of fat and musculoskeletal tissue. For men, the norm is 9 - 15% fat of total body weight, and for women - from 12 to 20%.
Quetelet index
Knowing the Body Mass Index (BMI), you can judge whether you are obese or underweight. The index is calculated for adult men and women from 20 to 65 years old. Results may be false for pregnant and breastfeeding women, athletes, the elderly and adolescents (under 18 years of age). Among the many different methods for calculating ideal weight, the most popular method is the height-weight indicator, body mass index - Quetelet index.
Formula: body weight in kg divided by height in meters squared B/(P*P) For example: height 170 cm, weight 65 kg. So 65: (1.7 * 1.7) = 22.5
The norm for men is 19-25. For women - 19-24.
| Risk of comorbidities | ||
| Less than 18.5 | Underweight | Low (increased risk of other diseases) |
| 18.5 – 24.9 | Normal body weight | Ordinary |
| 25.0 – 29.9 | Excess body weight (pre-obesity) | Elevated |
| 30.0 – 34.9 | Obesity I degree | High |
| 35.0 – 39.9 | Obesity II degree | Very tall |
| 40.0 or more | Obesity III degree | Extremely high |
The Quetelet index shows quite well the amount of fat in the body, but does not indicate how fat is distributed, in other words, it does not provide a visual or aesthetic picture. But you can test your body for perfection using one more formula.
The distribution of fat throughout the body is determined by the ratio: waist volume (at the level of the navel) divided by the volume of the buttocks.
- Norm for men: 0.85
- For women: 0.65 - 0.85.
Does age affect height-weight ratio?
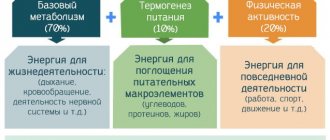
The answer is clear. Yes, of course it does. It has been proven that the weight of men and women should gradually increase with age - this is a normal physiological process. The kilograms that some people consider “extra” may not actually be so. You can use a formula based on age to determine your optimal weight.
P is height in this case, and B is age in years. Body weight = 50 + 0.75 (P - 150) + (B - 20) : 4
| Height in cm | Age | ||||||||||||||
| 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | |||||||||||
| Floor | |||||||||||||||
| M | AND | M | AND | M | AND | M | AND | M | AND | ||||||
| 150 | 51.3 | 48.9 | 56.7 | 53.9 | 58.1 | 58.5 | 58.0 | 55.7 | 57.3 | 54.8 | |||||
| 152 | 53.1 | 51.0 | 58.7 | 55.0 | 61.5 | 59.5 | 61.0 | 57.6 | 60.3 | 55.9 | |||||
| 154 | 55.3 | 53.0 | 61.6 | 59.1 | 64.5 | 62.4 | 63.8 | 60.2 | 61.9 | 59.0 | |||||
| 156 | 58.5 | 55.8 | 64.4 | 61.5 | 67.3 | 66.0 | 65.8 | 62.4 | 63.7 | 60.9 | |||||
| 158 | 61.2 | 58.1 | 67.3 | 64.1 | 70.4 | 67.9 | 68.0 | 64.5 | 67.0 | 62.4 | |||||
| 160 | 62.9 | 59.8 | 69.4 | 65.8 | 72.3 | 69.9 | 69.7 | 65.8 | 68.2 | 64.6 | |||||
| 162 | 64.6 | 61.6 | 71.0 | 68.5 | 74.4 | 72.2 | 72.7 | 68.7 | 69.1 | 66.5 | |||||
| 164 | 67.3 | 63.6 | 73.9 | 70.8 | 77.2 | 74.0 | 75.6 | 72.0 | 72.2 | 70.7 | |||||
| 166 | 68.8 | 65.2 | 74.5 | 71.8 | 78.0 | 76.6 | 76.3 | 73.8 | 74.3 | 71.4 | |||||
| 168 | 70.8 | 68.5 | 76.2 | 73.7 | 79.6 | 78.2 | 79.5 | 74.8 | 76.0 | 73.3 | |||||
| 170 | 72.7 | 69.2 | 77.7 | 75.8 | 81.0 | 79.8 | 79.9 | 76.8 | 76.9 | 75.0 | |||||
| 172 | 74.1 | 72.8 | 79.3 | 77.0 | 82.8 | 81.7 | 81.1 | 77.7 | 78.3 | 76.3 | |||||
| 174 | 77.5 | 74.3 | 80.8 | 79.0 | 84.4 | 83.7 | 82.5 | 79.4 | 79.3 | 78.0 | |||||
| 176 | 80.8 | 76.8 | 83.3 | 79.9 | 86.0 | 84.6 | 84.1 | 80.5 | 81.9 | 79.1 | |||||
| 178 | 83.0 | 78.2 | 85.6 | 82.4 | 88.0 | 86.1 | 86.5 | 82.4 | 82.8 | 80.9 | |||||
| 180 | 85.1 | 80.9 | 88.0 | 83.9 | 89.9 | 88.1 | 87.5 | 84.1 | 84.4 | 81.6 | |||||
| 182 | 87.2 | 83.3 | 90.6 | 87.7 | 91.4 | 89.3 | 89.5 | 86.5 | 85.4 | 82.9 | |||||
| 184 | 89.1 | 85.5 | 92.0 | 89.4 | 92.9 | 90.9 | 91.6 | 87.4 | 88.0 | 85.8 | |||||
| 186 | 93.1 | 89.2 | 95.0 | 91.0 | 96.6 | 92.9 | 92.8 | 89.6 | 89.0 | 87.3 | |||||
| 188 | 95.8 | 91.8 | 97.0 | 94.4 | 98.0 | 95.8 | 95.0 | 91.5 | 91.5 | 88.8 | |||||
| 190 | 97.1 | 92.3 | 99.5 | 95.8 | 100.7 | 97.4 | 99.4 | 95.6 | 94.8 | 92.9 | |||||
Broca's formula: identifying height-age-weight relationships
One of the most popular methods for calculating ideal weight is Brock's formula. It takes into account the ratio of height, weight, body type and age of a person.
Brock's formula for people under 40 years old is “height (in cm) minus 110″, after 40 years – “height (in cm) minus 100″.
At the same time, people with an asthenic (thin-boned) body type must subtract 10% from the result, and people with a hypersthenic (broad-boned) body type must add 10% to the result.
How to determine your body type?
Body types are usually divided into THREE types: normosthenic, hypersthenic and asthenic. In order to find out what your body type is, just measure the circumference of the thinnest place on your wrist with a centimeter. The resulting circumference in centimeters will be the necessary indicator (Soloviev index).
| Solovyov index | Body type | Typical for this body type | |
| for men | for women | ||
| 18-20 cm | 15-17 cm | normosthenic (normal) | the physique is distinguished by the proportionality of the main dimensions and their correct ratio |
| more than 20 cm | more than 17 cm | hypersthenic (wide-boned) | In people with a hypersthenic (broad-boned) body type, the transverse dimensions of the body are much larger than in normosthenics and especially asthenics. Their bones are thick and heavy, their shoulders, chest and hips are wide, and their legs are short. |
| less than 18 cm | less than 15 cm | asthenic (thin-boned) | In people with an asthenic (thin-boned) body type, longitudinal dimensions prevail over transverse ones: long limbs, thin bones, long, thin neck, muscles are poorly developed. |
Nagler's formula for height and weight ratio
There is a Nagler formula that allows you to calculate the ideal ratio of weight and height. For 152.4 cm of height there should be 45 kilograms of weight. For every inch (that is, 2.45 cm) over 152.4 cm there should be another 900 grams, plus another 10% of the resulting weight.
John McCallum's formula for girth ratio
One of the best formulas, created by expert methodologist John McCallum. McCallum's formula is based on measuring the circumference of the wrist.
- 6.5 wrist circumference is equal to chest circumference.
- 85% of the chest circumference is equal to the hip circumference.
- To get your waist circumference, you need to take 70% of your chest circumference.
- 53% of the chest circumference is equal to the hip circumference.
- For the neck circumference you need to take 37% of the chest circumference.
- The biceps circumference is about 36% of the chest circumference.
- The girth for the lower leg is slightly less than 34%.
- The forearm circumference should be equal to 29% of the chest circumference.
But not everyone’s physical data will exactly correspond to these ratios; the numbers have an average, statistical average value.
A few more options for height and weight ratios
- The physique is considered ideal if the waist circumference is 25 cm less than the hip circumference, and the hip circumference is approximately equal to the chest circumference.
- The waist circumference should be equal to “height in centimeters - 100”. That is, a woman with a height of 172 cm will be proportionally built if her waist circumference is 72 cm, her hip and waist circumference is about 97 cm, that is, if she wears a clothing size of 48.
- If the hip circumference is less than the chest circumference, and the waist circumference is 20 cm less than the hip circumference, then this figure is called an “apple”. If the chest circumference is less than the hip circumference, and the waist circumference is 30 cm or more less than the hip circumference, this is a pear-shaped figure.
- For women and girls of average height - from 165 to 175 cm - this observation turned out to be fair. Their waist circumference in centimeters is approximately equal to their weight in kilograms. One kilogram of weight loss results in a decrease in waist size of one centimeter.
Methods for calculating body fat percentage
Many people want to get rid of fat as much as possible. But in fact, it performs many important functions, and the body cannot live without fat at all. In women, with a lack of fat mass, the menstrual cycle and the functioning of the reproductive system are disrupted. Fat also regulates energy balance and performs protective and heat-insulating functions.
For the female body, 15-31% body fat is considered normal, and for the male body - 14-25%. Methods for determining the amount of fat mass in the body:
- Special floor scales-analyzers with measurement of fat percentage. A simple but not very accurate method. To determine the percentage, just step on the scale and look at the displayed values.
- Caliper. A special device that allows you to measure the thickness of the fat fold. The value is compared with a special table, from which the percentage of fat is determined. The fold is measured 10 cm to the right of the navel, approximately 3-4 cm from the femur. The fold must be pinched and measured with a caliper.
- Hydrostatic weighing. The most accurate, but difficult to perform method, since it is necessary to contact a specialized institution. The measurement is made using a bathtub into which a person is immersed. Then the percentage of fat is determined by the volume of displaced liquid.
Another simple way to measure your body fat percentage is to compare yourself to a photo of your body with different amounts of body fat.
It is enough to find in the photo the picture that most closely resembles the outline of your figure. The method is not very accurate, but it allows you to determine how the body looks from the outside.
Don't miss interesting news and events in the telegram channel: https://tlgg.ru/fitbarnews